Research Interests

  Mathematical and Computational Biology
  Mathematical Oncology and Medical application
  Multi-scale modeling and simulations
  Stochastic modeling and Uncertainty Quantification
  Numerical PDE and Scientific computing

Optimization of patient specific scanning schedule for radiotherapy

Mathematical modeling of cell based immunotherapy, CAR T-cell therapy

Mathematical modeling of therapeutic neural stem cells to sites of brain tumors and injury

Neural stem cells (NSC) have been shown to be a safe and effective means of treatment of primary brain tumors as well as traumatic brain injury. NSCs have demonstrated tropism to remote sites of tumor or injury in the brain, and have also been shown to migrate along anisotropic white matter tracts. NSCs may be delivered through several routes of administration, including intracerebral, intrathecal, and intranasal injection. This project aims to use mathematical modeling of chemotaxis-driven migration combined with anatomical features of the brain to predict--and subsequently improve--the efficiency of administration of NSCs to sites of tumor or injury. The models will be calibrated from pre-clinical animal models and compared with data collected from patients treated at City of Hope.

Continuum Cell State models from Single-cell Gene Sequencing Data

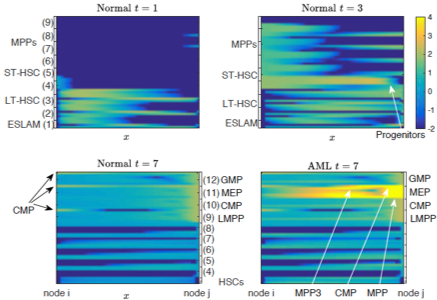
Single-cell RNA sequencing data (scRNA-seq) data provides the gene expression level that is in the dimensionality of O(10⁵) per each individual cell. By applying dimension reduction techniques, the data reveals a continuum cell state, that changes the classical view of cell biology assuming discrete cell states. We first study whether the assumption of continuum cell states yields distinct results from discrete cell state models, particularly in the context of anti-cancer drug resistance [11], by comparing the binary cell state model of drug-sensitive and drug-resistant to the continuum resistance model. Assuming continuous state may result in different dynamics when compared with the predictions of classical discrete models, and we classify the continuum models when they yield different dynamical patterns in the emerging heterogeneity in response to chemotherapy. Further, we develop a continuum cell state model using the gene data of hematopoietic stem cells (HSC) [10]. Diffusion mapping is applied to the data to reduce dimensionality. The trajectories of cell states in the continuum differentiation space are abstracted in the first few principal diffusion component space as a graph, then modeled as directed and random movement on the graph with PDEs. We simulate normal and abnormal differentiation processes (e.g. acute myeloid leukemia (AML) progression), and predict the emergence of cells in novel intermediate states of differentiation, that is consistent with the experiments of AML mouse mode.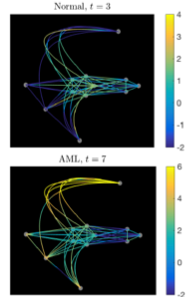

Modeling Dynamics of Drug Resistance and Spatial Heterogeneity in Tumor

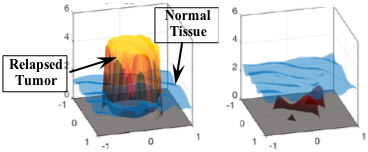
Drug resistance is a major challenge to successful cancer treatments. For a better understanding of chemotherapy-induced selection of drug-resistant traits during tumor growth, we develop a mathematical model to study the dynamics of drug resistance in solid tumor [7,9]. Our model follows the dynamics of the tumor, assuming that the cancer cell population depends on a phenotype variable that corresponds to the resistance level to a cytotoxic drug. The model successfully integrates the phenotype structured approach with an asymmetric tumor growth model in space. Through analysis and simulations, we study the impact of spatial and phenotypic heterogeneity on the tumor growth under chemotherapy. We demonstrate that heterogeneous cancer cells may emerge due to the selection dynamics of the environment, and our model predicts multiple resistant traits emerging at different locations within the tumor. Moreover, a higher dosage of the cytotoxic drug may delay a relapse, yet, when this happens, a more resistant trait emerges. An estimation of expansion rate of the tumor boundary and the time of relapse are provided as well.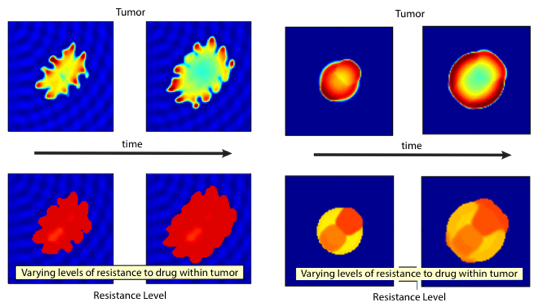

Figure. Various growth patterns predicted
by the model (top) and the corresponding
level of mean resistant trait (bottom) [9].

Study of Combination Therapy in Cancer Treatments

Designing effective anti-cancer strategies can be enhanced by mathematical models and techniques. We model and study potential combination and scheduling of multiple drugs with different mechanisms to overcome drug resistance. In the following series of work, we focus on developing combination therapies while taking account of the drug-resistant population into the model. We first study the effectiveness of a combination of cytotoxic and cytostatic drugs when the cancer cells consist of heterogeneous cell population in resistance to chemotherapy [7]. In particular, by aiming at minimizing the growth rate of the most resistant trait, we show that the resistant cancer cells can be eliminated by the proposed combination of treatment. Moreover, an adaptive therapy can be administered by considering the maximal fitness traits. In addition, we study a combination of cytotoxic and targeted drugs while considering resistance to both drugs [12]. We demonstrate the effectiveness of targeted drugs when cell competition between cancer cells and normal tissue cells are aggressive, and propose alternating scheduling based on the ratio of resistant cells to each drug.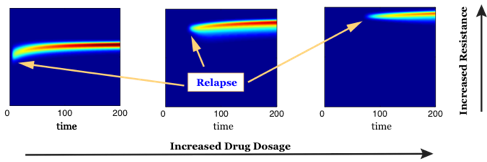

Modeling and Simulation of Stochastic System with Colored Noise

Evolution equations of the response-excitation probability density function (PDF) generalize the existing kinetic equations and enable us to compute the stochastic solution of systems driven by random excitations including colored noise [1]. We develop an efficient high-order numerical method for this system, involving a non-conforming adaptive discontinuous Galerkin (DG) method in the response space and the probabilistic collocation method (PCM) in the excitation variables [2]. In addition to showing that the system agrees with the effective Fokker-Planck equation in the white noise limit, we study chaotic and bi-stable oscillator problems and Burgers equation subjected to colored noise [2,4]. The algorithm captures stiff and localized solutions accurately.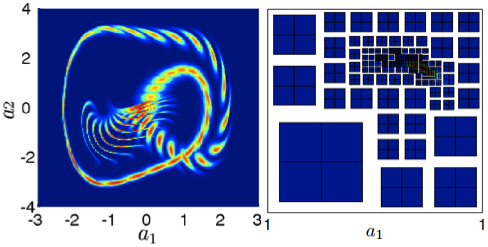

Figure. Time evolution of the response
PDF of Duffing oscillator and a snapshot
of adaptive grid.

Efficient Numerical methods for High-dimensional Stochastic Systems

High-dimensionality is one of the major challenges in uncertainty quantification. In particular, kinetic models and simulations of realistic physical systems are generally more expensive than moment-based methods, while they provide the PDF that contains complete statistical structure of the stochastic dynamics. Thus, we develop several algorithms based on well-known approximations for high-dimensional functions, namely, the sparse grid (SG) approximation, high-dimensional model representation (ANOVA) and tensor decomposition [6]. The ANOVA expansion superimposes the solution regarding the low-order interaction, while the tensor decomposition, approximates the solution as a series of low-dimensional functional products. The algorithms based on these methods reduce the computation into a series of lower-dimensional operations. In addition to high-dimensional kinetic simulation, we develop an adaptive reduced basis collocation method to efficiently solve high-dimensional parameterized stochastic PDEs [8]. The method employs two stages of adaptive procedure based on PCM and ANOVA decomposition by exploring the low rank structure of the solution in the stochastic domain. The method enables efficient simulation of anisotropic and irregular stochastic systems.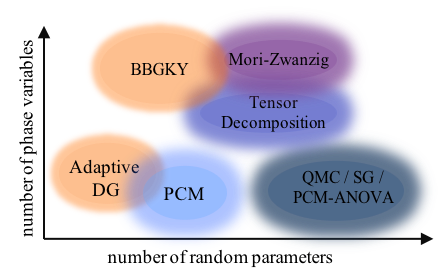

Figure. Range of applicable numerical methods for the kinetic
equation with random parameters in terms of dimensionality
in the phase variables and the number of parameters.

Representation of Multiple Correlated Stochastic Processes

The Karhunen-Loeve (KL) expansion is an effective mathematical representation of a non-stationary stochastic process used in stochastic simulations. However, the representation is limited to a single process or ensembles of statistically independent processes. We extend the KL expansion to model multiple correlated non-stationary stochastic processes focused on the mutual correlations [3]. Two methods, muKL and mCKL, have been developed, where the former is optimal in mean square error, and the latter requires less computational cost. The convergence of the expansion is proven analytically and demonstrated in numerical examples involving Gaussian processes as well as fractional Brownian motions. The proposed methods can be readily employed in stochastic simulation involving multi-correlated processes and mutually correlated data-driven problems for dimension reduction. Moreover, we develop local KL expansion to accompany domain decomposition methods in the physical space [5]. The algorithm decomposes the series expansion to local sub-domains while preserving the global statistical structure.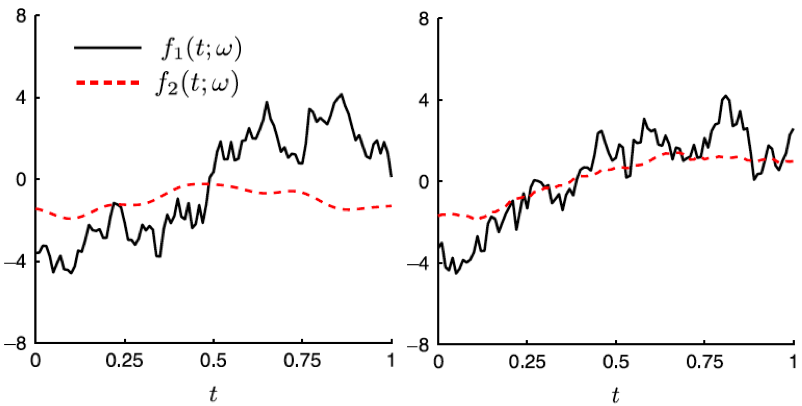

Figure. Sample trajectories of two stochastic processes
generated by mKL method that are independent (left)
and strongly correlated (right).

  [11] H. Cho, D. Levy, 'Modeling continuous levels of resistance to multidrug therapy in cancer', https://arxiv.org/abs/1806.07557, Appl.Math.Model., 2018
  [10] H. Cho, K. Ayers, L. DePillis, Y-H. Kuo, J. Park, A. Radunskaya, R. Rockne, ‘Modeling acute myeloid leukemia in a continuum of differentiation states’, Lett.Biomath., 2018
  [9] H. Cho, D. Levy, 'Modeling the chemotherapy-induced selection of drug-resistant traits during tumor growth', J. Theor. Biol. 436(7), 2018
  [8] H. Cho, H. Elman, ‘Adaptive reduced basis collocation method based on PCM for anisotropic stochastic PDEs’, Int. J. Uncertain. Quantif. 8(3), 2018
  [7] H. Cho, D. Levy, 'Modeling the dynamics of heterogeneity of solid tumors in response to chemotherapy', Bull. Math. Bio. 79(12), 2017
  [6] H. Cho, D. Venturi, G. E. Karniadakis, ‘Numerical methods for high-dimensional probability density function equations', J. Comput. Phys. 305, 2016
  [5] H. Cho, X. Yang, D. Venturi, G. E. Karniadakis, 'Algorithms for propagating uncertainty across heterogeneous domains', SIAM J. Sci. Comput. 37(6), 2015
  [4] H. Cho,  D. Venturi, G. E. Karniadakis, ‘Statistical analysis and simulation of random shocks in Burgers turbulence’, Proc. R. Soc. A, 470(2171), 2014.
  [3] H. Cho, D. Venturi, G. E. Karniadakis, ‘Karhunen-Loeve expansion for multi-correlated stochastic processes’, Probabilistic Eng. Mech., 2013  
  [2] H. Cho, D. Venturi, G. E. Karniadakis, ‘Adaptive discontinuous Galerkin method for response-excitation PDF equations’, SIAM J. Sci. Comput. 2013 
  [1] D. Venturi, T. P. Sapsis, H. Cho, G. E. Karniadakis, ‘A computable evolution equation for the joint response-excitation probability density function of stochastic dynamical systems', Proc. R. Soc. A 2012 

 

Check out some of my talks! -> SIAM-UQ12, SIAM-UQ14
Check out some of my posters! -> IMO16, IMA18